二叉搜索树可视化

二叉搜索树（Binary Search Tree，简称 BST）是一种特殊的二叉树数据结构，它具有以下特点：

  • 每个节点都包含一个值（键）；
  • 左子树中的所有节点值都小于当前节点的值；
  • 右子树中的所有节点值都大于当前节点的值；
  • 左右子树也都是二叉搜索树。

二叉搜索树可视化

本页面提供了一个交互式的二叉搜索树可视化工具，帮助大家深入理解二叉搜索树的结构和操作原理。

树的初始化

在开始使用可视化工具时，可以先初始化一棵二叉搜索树。本页面提供了灵活的初始化选项，允许用户指定树的大小，范围可以从1个节点到50个节点不等。这种范围的设定既能展示简单的树结构，也能演示较为复杂的情况。

初始化支持两种不同的数值生成方式。第一种是随机数值模式，系统会在1到1000的范围内随机生成不重复的数字作为节点值。这种模式能够模拟真实世界中的随机数据情况，展示树在不同数据分布下的形态。第二种是顺序数值模式，系统会按照0,1,2...的顺序生成节点值。这种模式特别有助于理解二叉搜索树在处理有序数据时可能出现的退化情况。

可视化工具实现了二叉搜索树的三个核心操作，每个操作都能实时展示树结构的变化过程。

搜索和插入

搜索操作展示了二叉搜索树高效查找的优势。在二叉搜索树中查找一个值时，我们从根节点开始，利用二叉搜索树的特性（左子树所有节点值小于根节点，右子树所有节点值大于根节点）来缩小搜索范围：

  • 如果目标值等于当前节点的值，则找到目标节点
  • 如果目标值小于当前节点的值，则在左子树中继续搜索
  • 如果目标值大于当前节点的值，则在右子树中继续搜索

通过这种方式，每次比较都会排除掉约一半的节点，使得搜索效率大大提高。用户可以输入任意值进行搜索，系统会通过高亮显示完整的搜索路径，直观地展示从根节点到目标位置的整个查找过程。

插入操作允许用户向二叉搜索树中添加新的节点。系统会自动寻找合适的位置并保持二叉搜索树的特性。插入过程如下：

  1. 从根节点开始，将新值与当前节点的值比较
  2. 如果新值小于当前节点的值，则往左子树方向继续寻找
  3. 如果新值大于当前节点的值，则往右子树方向继续寻找
  4. 当到达一个空位置时，就是新节点应该插入的位置

如下图演示，用户可以清晰地观察到新节点是如何一步步找到其正确位置的。这个过程展示了二叉搜索树如何在保持其基本性质（有序性）的同时，动态地生长和扩展。

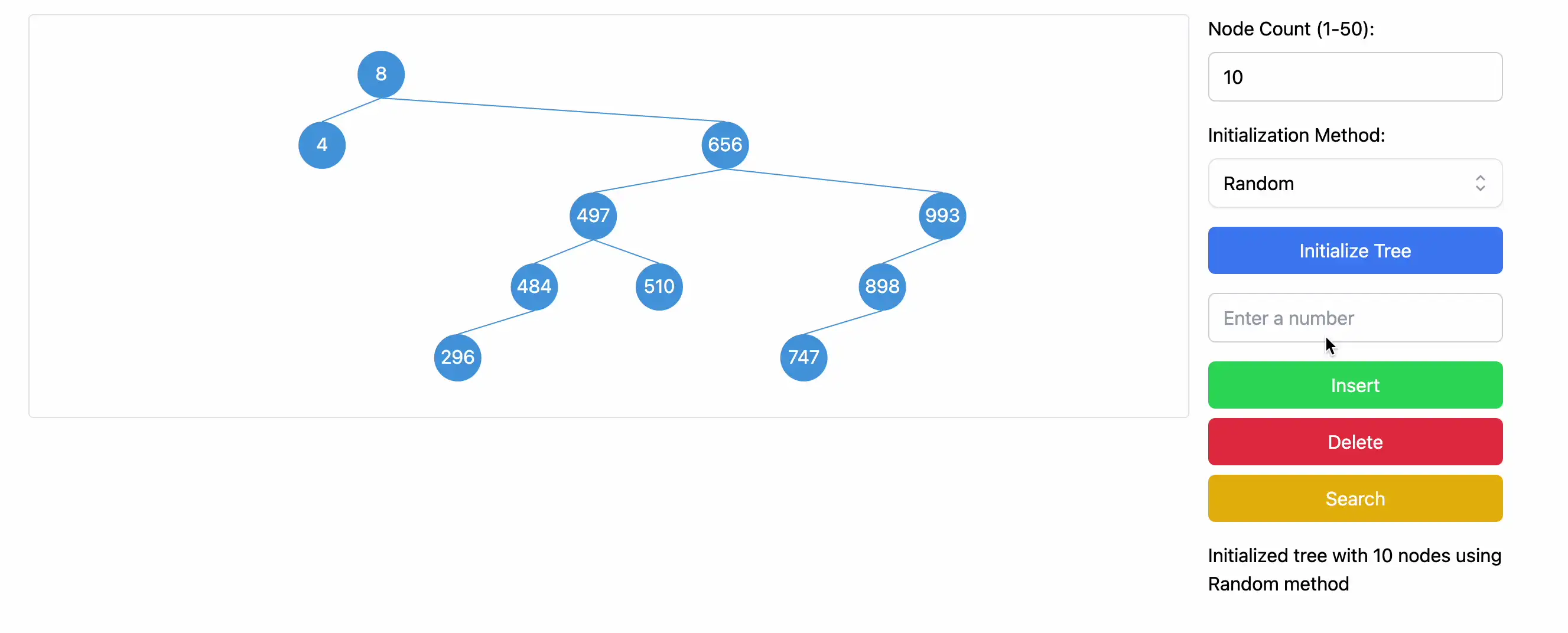
二叉搜索树插入操作的情景

插入操作的一个重要特点是，它总是在树的叶子节点位置添加新节点，这样可以最小程度地影响树的现有结构。同时，由于遵循二叉搜索树的性质进行插入，整个过程自然而然地维持了树中所有节点的正确顺序。

删除操作

二叉搜索树的删除操作是三种基本操作中最复杂的一个，因为删除节点可能会破坏树的结构，需要重新调整以维持二叉搜索树的性质。删除操作根据待删除节点的子节点情况，分为三种不同的情况。

  1. 删除叶子节点：这是最简单的情况。当要删除的节点是叶子节点时，我们首先需要沿着树向下搜索要删除的节点。找到目标节点后，只需要将其父节点对应的指针（左子节点或右子节点）设为 null 即可。如果删除的是根节点，则直接将 root 设为 null。这种情况不会影响到树的其他部分，因为叶子节点没有任何子节点，不需要处理节点的重新连接。

  2. 删除只有一个子节点的节点：当要删除的节点只有一个子节点时，我们需要先搜索到要删除的节点，并确定该节点是其父节点的左子节点还是右子节点。然后，将被删节点的唯一子节点（可能是左子节点或右子节点）直接连接到被删节点的父节点对应位置。如果删除的是根节点，则将其唯一的子节点设为新的根节点。这种情况下，树的结构变化较小，只需要重新连接一个节点。

  3. 删除有两个子节点的节点：这是最复杂的情况，因为我们需要找到一个合适的节点来替换被删除的节点，以保持二叉搜索树的性质。删除过程如下：

    1. 首先需要找到要删除节点的后继节点，也就是右子树中的最小节点。查找后继节点的过程是：先访问要删除节点的右子节点，然后不断往左子节点方向走，直到找到没有左子节点的节点。这个节点就是后继节点，它的值刚好大于被删除节点的值。
    2. 找到后继节点后，将其值复制到被删除节点的位置。然后删除后继节点本身。由于后继节点最多只有一个右子节点（不可能有左子节点，否则就不是最小节点了），所以删除后继节点可以按照情况一或情况二的方式处理。

下图演示了删除有 1 个子节点的节点的动画过程。

二叉搜索树删除有1个子节点的节点

时间复杂度分析

二叉搜索树的性能表现与树的结构密切相关。在理想情况下，即树保持较好平衡时，二叉搜索树能够提供非常高效的操作性能。

在平均情况下，二叉搜索树的基本操作都能达到对数级的时间复杂度。查找操作的时间复杂度为O(log n)，这是因为每次比较都会将搜索范围缩小一半，形成了典型的二分查找过程。插入操作同样具有O(log n)的时间复杂度，因为需要先进行查找来确定插入位置，然后执行常数时间的节点链接操作。删除操作虽然可能涉及到后继节点的查找和树的重组，但其时间复杂度仍然保持在O(log n)级别。

然而，在最不理想的情况下，当二叉搜索树退化为一个链表时，其性能会显著下降。这种情况通常发生在按照有序序列插入节点时，例如依次插入1,2,3,4,5这样的序列。此时，每个新节点都会被插入到右子树的最底层，导致树完全失去平衡，变成一个单链表结构。在这种退化情况下，所有基本操作的时间复杂度都会退化到O(n)，因为每次操作都需要遍历整个链表才能完成。

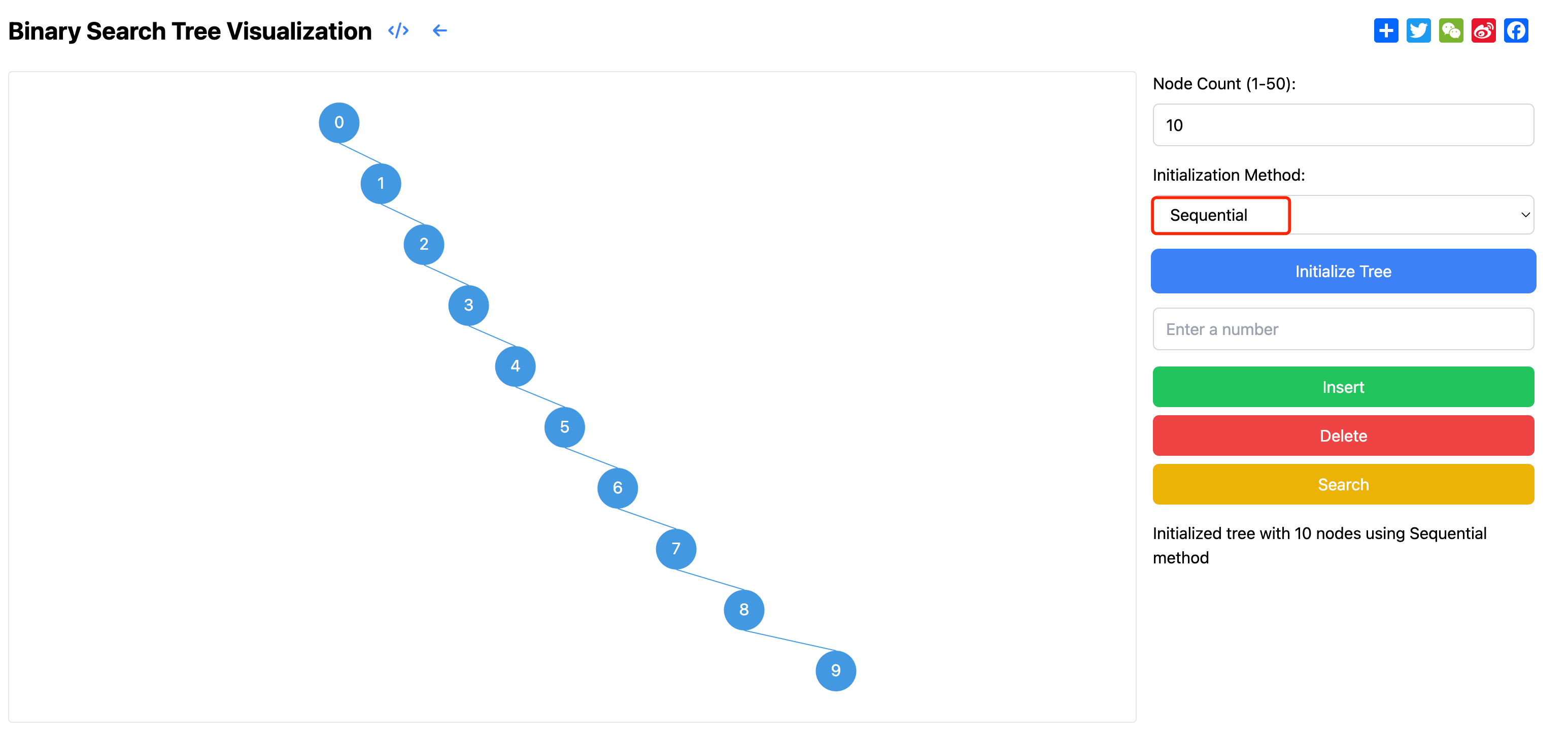
二叉搜索树顺序插入时的情景

此外，在需要频繁修改的场景中，大量的插入和删除操作可能导致树结构逐渐失衡。虽然可以通过定期重建树来解决这个问题，但这种方案会带来额外的性能开销。这个特点使得普通的二叉搜索树不太适合用于需要频繁更新的数据存储场景。

其他替代数据结构

当二叉搜索树无法满足性能需求时，我们可以考虑一些更高级的数据结构。这些结构都是在二叉搜索树基础上的改进和优化，每种结构都有其特定的应用场景。

AVL树：AVL树是最早被发明的自平衡二叉搜索树，它通过严格控制左右子树的高度差来保持平衡。在AVL树中，任何节点的左右子树高度差不超过 1，这种严格的平衡条件确保了树的高度始终保持在O(log n)级别。每次插入或删除操作后，AVL树都会通过旋转操作来恢复平衡。

红黑树：是一种弱平衡的二叉搜索树，它通过为节点染色（红色或黑色）并保持特定的颜色规则来维持平衡。相比AVL树，红黑树的平衡条件更为宽松，它只确保从根到叶子的最长路径不超过最短路径的两倍。这种设计在保证了足够好的性能的同时，大大减少了维护平衡所需的操作次数。

正是因为这种平衡和性能的良好折中，红黑树在实际工程中被广泛应用。例如，Java中的TreeMap和TreeSet，C++中的map和set，以及Linux内核中的完全公平调度器，都使用了红黑树作为底层数据结构。

B树和B+树：为磁盘等外部存储设备专门设计的多路搜索树。与二叉树不同，这些树的节点可以包含多个键值和子节点。B树的每个节点都可以存储数据，而B+树只在叶子节点存储数据，非叶子节点仅用作索引。这种结构设计可以显著减少磁盘I/O操作的次数。

跳表：跳表是一种基于链表的数据结构，它通过在每个节点中添加多层索引来加速查找操作。跳表的查找、插入和删除操作的时间复杂度均为O(log n)，这使得它在某些场景下可以替代平衡二叉搜索树。