A* 寻路可视化演示
可以通过本可视化页面来理解 A* 算法。页面加载后会有一个适当大小的网格,里面代表整个“地图”,每个网格代表的距离是相同的。
初始化的时候,会选择左下角网格为开始搜索位置(绿色小旗帜),右上角为终点位置(红色小旗帜),然后在地图中随机生成一些障碍物(灰色带 X 的网格)。
我们的目标是找到从起点到终点的最短路径,并且路径上不能有障碍物。
可以手动调整障碍物、起点和终点位置,然后点击“查找路径”按钮,查看搜索过程。
整个搜索过程会用动画演示,每一步的搜索结果会用不同的颜色标记。当最后找到一个最短路径后,会用绿色标记整条路径。
搜索过程中,还会用灰色和黄色来表示开放集和关闭集,这两个概念稍后解释。
A* 寻路算法
A* 算法是一种广泛使用的启发式寻路算法。这里启发的意思是说,从某个位置开始找路的时候,不是去随机遍历,而是利用一些已知信息,来估算每种选择的成本,然后选择成本最低的方向。
A* 寻路算法的核心思想如下:
- 使用启发式函数来估计从当前节点到目标节点的成本。
- 维护一个开放列表(待探索的节点)和一个关闭列表(已探索的节点)。
- 每次选择估计总成本最低的节点进行探索。
本页面可视化实现中,用二维数组表示网格,每个节点记录 f、g、h 值:
- g值(g-cost):从起点到当前节点的实际代价,反映已知路径的成本。通常是路径上的步数或边的权重之和,本页面因为是相同权重格子,所以直接用曼哈顿距离。
- h值(h-cost):从当前节点到目标节点的启发式估计值。启发式估计值通常是基于某种启发式函数(如曼哈顿距离、欧几里得距离等)计算的。
- f值(f-cost):从起点经过当前节点到达目标节点的总估计值。f = g + h。
搜索过程中,会维护一个开放集(待探索的节点)和一个关闭集(已探索的节点)。
- 开放集:包含所有已发现但尚未完全评估的节点,初始化的时候只用把开始节点加入。
- 关闭集:包含所有已评估的节点,初始化的时候为空。
这样算法不会重复评估已处理的节点,因为已经处理的都在关闭集中。另一方面,所有潜在的路径选择都被考虑,因为在开放集中。
这样整体搜索的步骤如下:初始化的时候,设置起点的g值为0,计算起点到终点的启发式估计值 h,计算起点的f值(f = g + h)。把起点放到开放集中,在主循环中,只要开放集不为空,就继续搜索。
每次从开放集中选择 f 值最小的节点作为当前节点,然后遍历当前节点的所有邻居:
- 忽略已在关闭集中的邻居;
- 计算从起点经过当前节点到达邻居的g值;
- 如果邻居不在开放集中,将其加入;
- 如果新路径不比旧路径更好,跳过;
- 更新邻居节点的父节点、g值、h值和f值;
最后如果开放集为空且未找到路径,则说明不存在最短路径。如果搜索的时候,f值最小的节点是终点,则说明找到最短路径。
最后只需要回溯重建最短路径即可。在搜索过程中,为每个探索的节点设置了 parent 属性,最后反向遍历 parent 属性即可。
整个 A* 搜索的流程如下图所示:
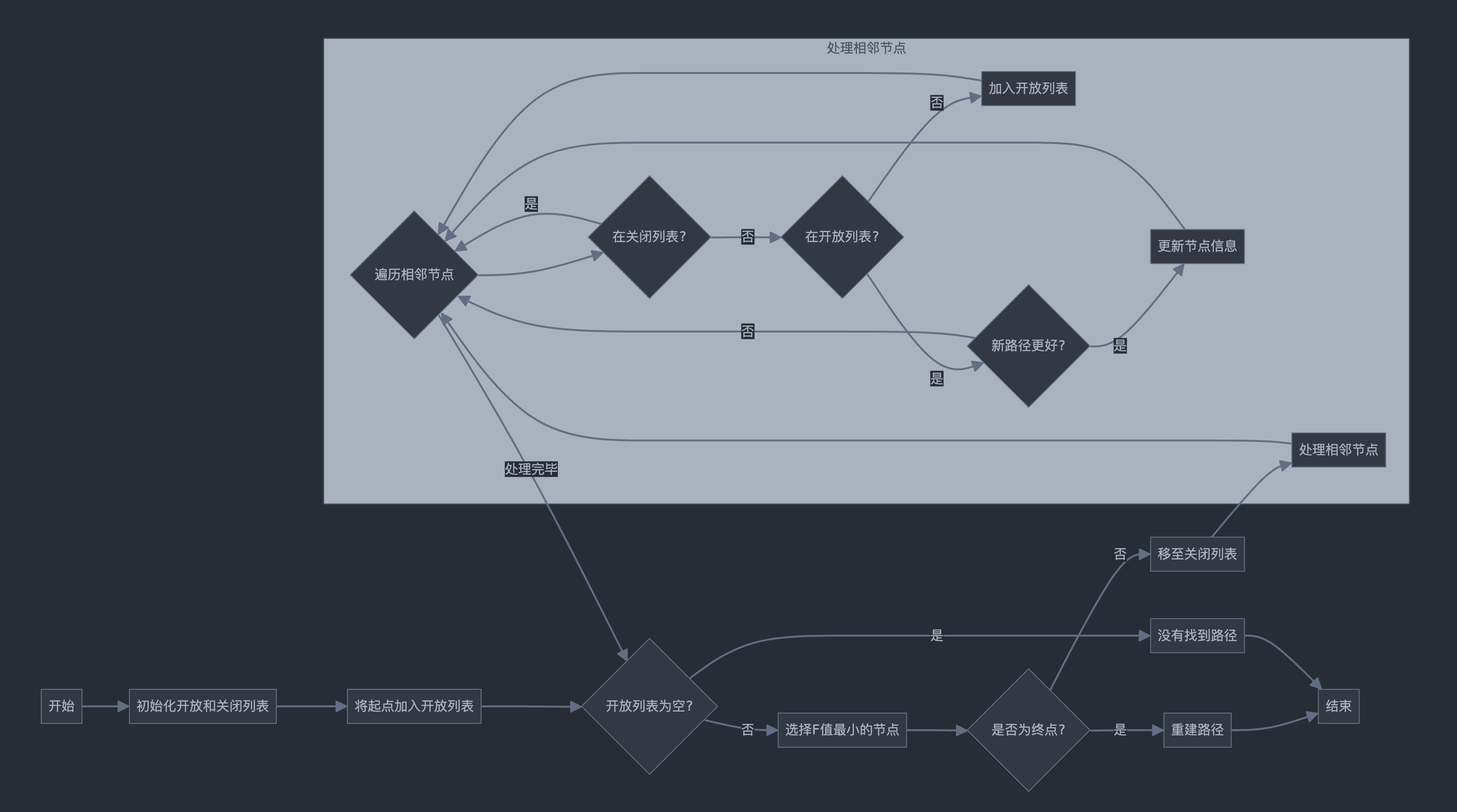
源码如下:
graph LR
A[开始] --> B[初始化开放和关闭列表]
B --> C[将起点加入开放列表]
C --> D{开放列表为空?}
D -->|是| E[没有找到路径]
D -->|否| F[选择F值最小的节点]
F --> G{是否为终点?}
G -->|是| H[重建路径]
G -->|否| I[移至关闭列表]
I --> J[处理相邻节点]
subgraph 处理相邻节点
J --> K{遍历相邻节点}
K --> L{在关闭列表?}
L -->|是| K
L -->|否| M{在开放列表?}
M -->|否| N[加入开放列表]
M -->|是| O{新路径更好?}
O -->|是| P[更新节点信息]
O -->|否| K
N --> K
P --> K
end
K --> |处理完毕| D
H --> Q[结束]
E --> Q
其他
和广度优先搜索路径相比,A* 算法可以更快地找到最短路径。因为广度优先搜索是盲目地沿着路径开始查找,直到遍历所有的可能路径。
而 A* 算法会利用启发式函数来估计从当前节点到目标节点的成本,从而更快地找到最短路径。具体可以从动画演示中看到这点区别。
与Dijkstra算法相比,A*算法只找到从指定源到指定目标的最短路径,而不是从指定源到所有可能目标的最短路径树。
这是使用特定目标导向启发式的必要权衡。对于Dijkstra算法,由于生成了整个最短路径树,所以每个节点都是一个目标,并且不可能有特定目标导向的启发式。