Dynamic Programming (Coin Change)

What is Dynamic Programming?

Dynamic Programming is a method of solving complex problems by breaking them down into simpler subproblems. Its core ideas are:

• Breaking complex problems into interrelated subproblems
• Solving the original problem by solving subproblems
• Storing results of solved subproblems to avoid repeated calculations

Problems that can be solved using dynamic programming typically have these characteristics:

1. Optimal Substructure: The optimal solution contains optimal solutions to subproblems
2. Overlapping Subproblems: The same subproblems appear repeatedly during the solving process
3. State Transition: Finding relationships between subproblems and solving them through state transition equations

When solving dynamic programming problems, we need to think and solve systematically following these steps:

1. Define States: First, consider how to describe the problem mathematically. Defining states is the most crucial step in the entire solving process, as it determines how we store and use calculation results. We need to carefully consider: What variables are needed to represent the problem? These states are usually stored in array form. A good state definition should completely describe the situation at a certain stage of the problem.

2. Find State Transition Equations: After defining states, we need to think about how states transition between each other. In other words, how to derive new states from known states. The state transition equation is the core of solving the problem - once you understand it, the problem is essentially solved.

3. Determine Initial States and Boundary Conditions: With the state transition equation, we need to determine the initial states of the problem. Additionally, we need to consider special cases, such as how to handle inputs of zero or negative numbers.

4. Solve Using State Transition Equations: The final step is the actual solving process. We usually calculate each state's value in a certain order (like from small to large). During this process, we use previously calculated state values to derive new state values through the state transition equation. Special attention must be paid to the calculation order to ensure that all dependent states are calculated before computing a new state.

The Coin Change Problem

Let's understand dynamic programming through a common real-life scenario.

The Coin Change Problem comes from a common scenario in daily life. Given a set of different coin denominations and a target amount, our goal is to calculate the minimum number of coins needed to make up the target amount.

First, let's think about what we need to solve: "the minimum number of coins needed to make up a certain amount." We can define state dp[i] as: the minimum number of coins needed to make up amount i.

Now think: How do we derive new states from known states?

Suppose we're calculating dp[i], which is the minimum number of coins needed to make up amount i. We can break this down into subproblems:

1. If we choose to use a coin of value m, then the problem transforms into: the minimum number of coins needed to make up amount (i-m), plus this new coin;
2. Since we're looking for the minimum number of coins, we need to take the minimum value among all possible coin choices;

Therefore, the state transition equation is as follows, where m iterates through all available coin denominations:

dp[i] = min(dp[i-m] + 1)

Then we need to determine initial states and boundary conditions:

1. When the amount is 0, no coins are needed, so dp[0] = 0;
2. For other amounts, initially set to infinity, indicating no solution found yet;
3. When calculating a state, we can only use a coin of value m when i ≥ m.

Now let's use this page's visualization tool to intuitively experience the dynamic programming solving process.

Dynamic Programming Visualization Tool Guide

This page's visualization tool is divided into two main areas. In the right settings panel, you can customize the problem parameters.

First, you can set the target amount you want to make up, with a default value of 11. Then, you can adjust the available coin denominations by adding or removing different coin values, with default values of 1, 2, and 5. After setting these parameters, you can use the control buttons to observe the solving process.

The control buttons offer two execution modes: If you want to understand each calculation step in detail, you can choose the "Step-by-Step" mode, where the system pauses at each step, allowing you to clearly observe how states transition. If you only care about the final result, you can choose the "Quick Complete" mode, which directly shows the complete solution.

In the left result display area, you'll see a dynamically updating table. This table shows the solution process for each amount from 0 to the target amount. For each amount, you can see three key pieces of information: the minimum number of coins needed, which coins were used (optimal combination), and how the current solution was derived from previous states.

To make the calculation process more intuitive, the system uses different color markers to highlight important information. The current calculation step is highlighted in yellow, allowing you to clearly track the calculation progress. When a better solution is found, the relevant state transition path is marked in green. Additionally, the system shows coin combinations graphically, letting you visually see how the optimal solution for each amount is composed of coins.

Let's look at a specific example. When we set the target amount to 11 and use coins of values 1, 2, and 5, the system will show the calculation process step by step. As shown below:

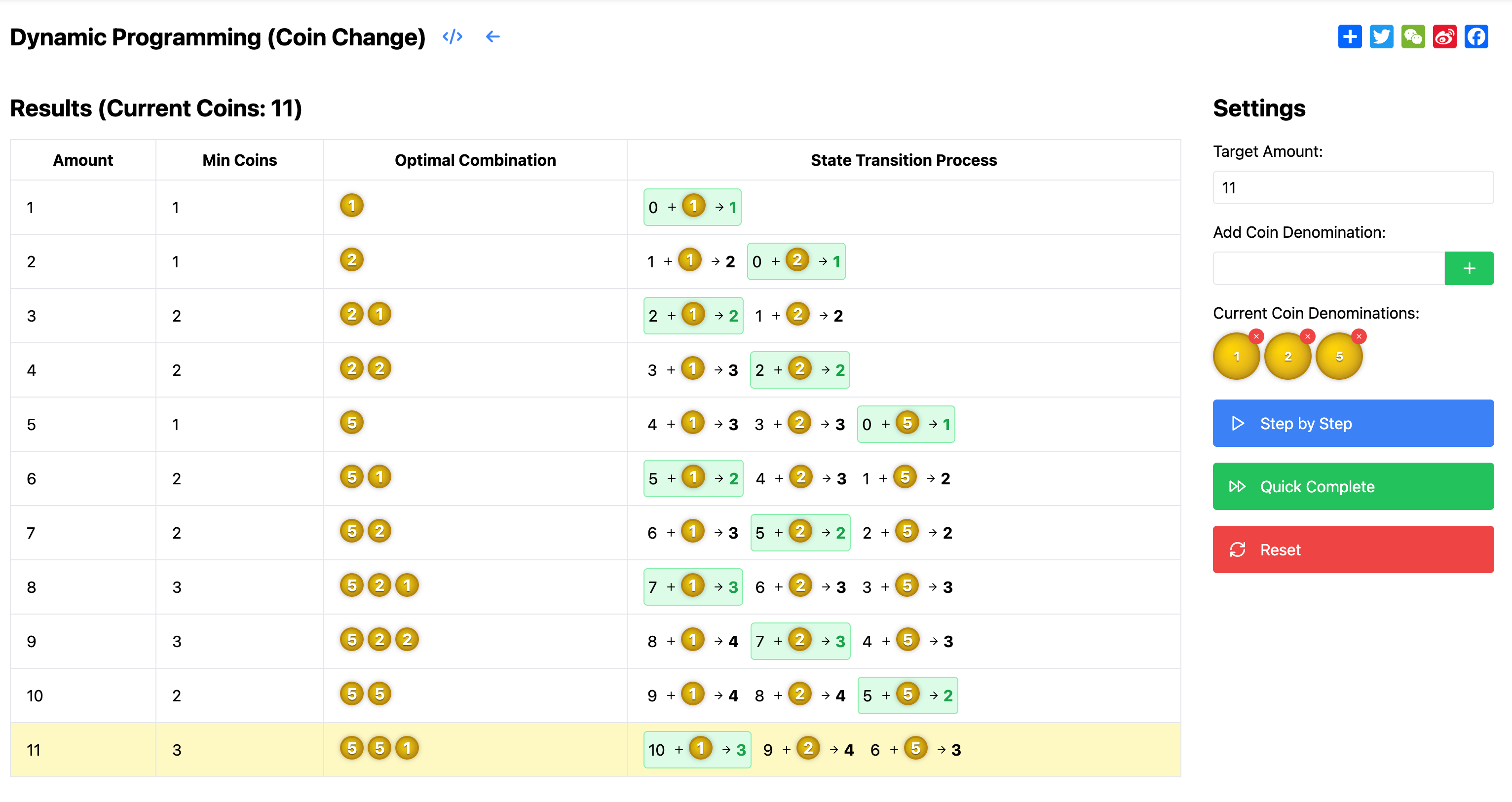
The optimal solution calculation process for each amount:

• dp[1] = min(dp[1-1] + 1) = dp[0] + 1 = 1
• dp[2] = min(dp[2-1] + 1, dp[2-2] + 1) = min(2, 1) = 1
• dp[3] = min(dp[3-1] + 1, dp[3-2] + 1) = min(2, 2) = 2
• dp[4] = min(dp[4-1] + 1, dp[4-2] + 1) = min(3, 2) = 2
• dp[5] = min(dp[5-1] + 1, dp[5-2] + 1, dp[5-5] + 1) = min(3, 3, 1) = 1

...and so on. Through this visualization, you can clearly understand the dynamic programming solving process, see how states transition step by step, and how the optimal solution is found. This helps in understanding the core ideas and solving approaches of dynamic programming.

Challenges in Dynamic Programming

While dynamic programming is a powerful problem-solving tool, it often faces several main challenges in practical applications:

Defining Good States: The most challenging part is often finding appropriate state definitions. A good state definition needs to meet two key requirements: it must completely describe the problem while remaining as simple as possible. Sometimes, seemingly reasonable state definitions might lead to difficulties in deriving state transition equations, requiring us to rethink the state definition approach.

Deriving State Transition Equations: Even with correctly defined states, finding the transition relationships between states remains difficult. We need to consider: Which previous states are related to the current state? How do we derive the current state from these states? Sometimes we might need to consider multi-dimensional state transitions, which greatly increases complexity.

Consider these classic dynamic programming problems and try to think of appropriate state definitions and state transition equations:

1. Edit Distance Problem: Given two strings, calculate the minimum number of operations needed to convert one string into another (can insert, delete, or replace characters).
2. Maximum Subarray Sum Problem: Given an integer array, find the contiguous subarray with the largest sum.
3. Knapsack Problem: Given a set of items, each with weight and value, how to choose items to maximize total value while staying within a weight limit.

When facing difficult problems, try these approaches to see if dynamic programming can help:

1. Start with the simplest examples, manually work through small-scale cases;
2. Try different state definitions until finding one that can fully express the complete problem;
3. Use diagrams to aid thinking, especially for problems involving intervals or multi-dimensional states;
4. Focus more on the state transition process rather than specific values;
5. Verify correctness in special cases, such as empty input or single-element cases.