Weight Matrix
| Inf | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| A | Inf | 10 | Inf | 4 | Inf | Inf |
| B | 10 | Inf | 8 | 2 | 6 | Inf |
| C | Inf | 8 | Inf | Inf | 1 | 5 |
| D | 4 | 2 | Inf | Inf | 6 | Inf |
| E | Inf | 6 | 1 | 6 | Inf | 12 |
| F | Inf | Inf | 5 | Inf | 12 | Inf |
Dijkstra's algorithm is a classic algorithm for solving the single-source shortest path problem in weighted graphs. It was proposed by Dutch computer scientist Edsger Dijkstra in 1956. In real life, this algorithm is widely used in navigation systems, network routing, and other scenarios.
For example, in map navigation, cities can be viewed as nodes in the graph, roads as edges, and distance or time as weights. Dijkstra's algorithm helps us find the shortest paths from a starting city to all other cities.
Dijkstra's Algorithm Principle
The core idea of Dijkstra's algorithm is to gradually extend the shortest paths to find the shortest distances from the starting point to all other nodes. It employs a greedy strategy, always selecting the unvisited node with the smallest distance for expansion.
The algorithm maintains two key data structures: a distance array 'dis' that records the shortest distances, and a vertex set 'T' that records nodes with confirmed shortest paths. Initially, the distance from the starting point to itself is set to 0, to all other vertices to infinity, and set T only contains the starting point.
In each iteration, the algorithm selects the vertex with the smallest distance from the unvisited vertices in the dis array and adds it to set T. The shortest path to this vertex is now confirmed. Then, the algorithm uses this newly added vertex as a transit point to check and update the path lengths from the starting point through this vertex to other vertices. If a shorter path can be found through this transit point, the distance value for the corresponding vertex in the dis array is updated.
This process continues until one of the following conditions is met:
- All vertices have been added to set T, indicating that the shortest paths to all reachable vertices have been confirmed;
- All remaining unvisited vertices have infinite distance values, indicating these vertices are unreachable from the starting point.
When the algorithm terminates, the dis array contains the shortest distances from the starting point to all other vertices, where vertices with infinite distance are unreachable from the starting point. Additionally, by recording predecessor nodes along the paths, we can reconstruct the specific shortest paths to all reachable vertices.
Finding it hard to understand? No worries, let's use the visualization tool to understand this process.
Visualization Operation Guide
This visualization tool is quite powerful, supporting the following features:
- You can select the starting node in the top-left corner. The default is node A, but you can choose different starting nodes to see how paths differ;
- Double-click on edges to modify their weights, you can modify weights, delete edges with the Del key after clicking them, or delete nodes with the Del key after clicking them. Observe how changing nodes, edges, and weights affects the shortest paths;
- During algorithm execution, the shortest paths are highlighted in green, and the weight matrix and each calculation step are displayed in real-time on the right;
- Supports step-by-step and automatic execution, with the ability to pause automatic execution using the pause button, making it easier to understand the algorithm's execution process.
Using this visualization tool, we can intuitively understand how Dijkstra's algorithm finds the shortest paths step by step. When edge weights are modified, the algorithm recalculates, helping us understand how different weights affect the shortest paths.
Specific Shortest Path Finding Process
For the undirected graph below, let's choose A as the starting node and see how the algorithm finds the shortest paths step by step.
Click next step, in the first step with A as the starting point, it records the shortest distances to each point through A.
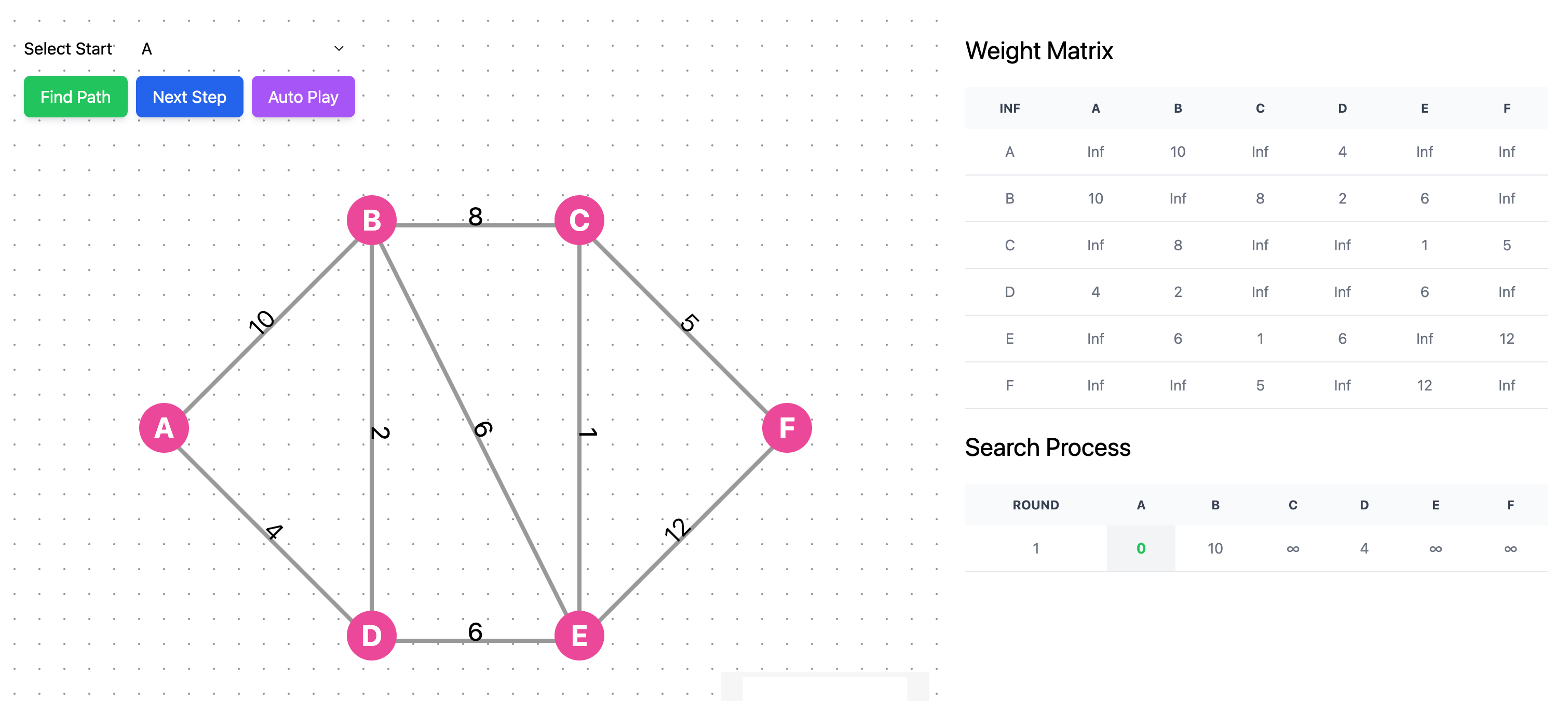
Continue clicking next step, and you'll see that from the unvisited vertices in the previous step, the vertex with the smallest distance is selected, which is vertex D with a distance of 4.
Using D as a transit point, update the distances from A through D to other vertices, as shown below:
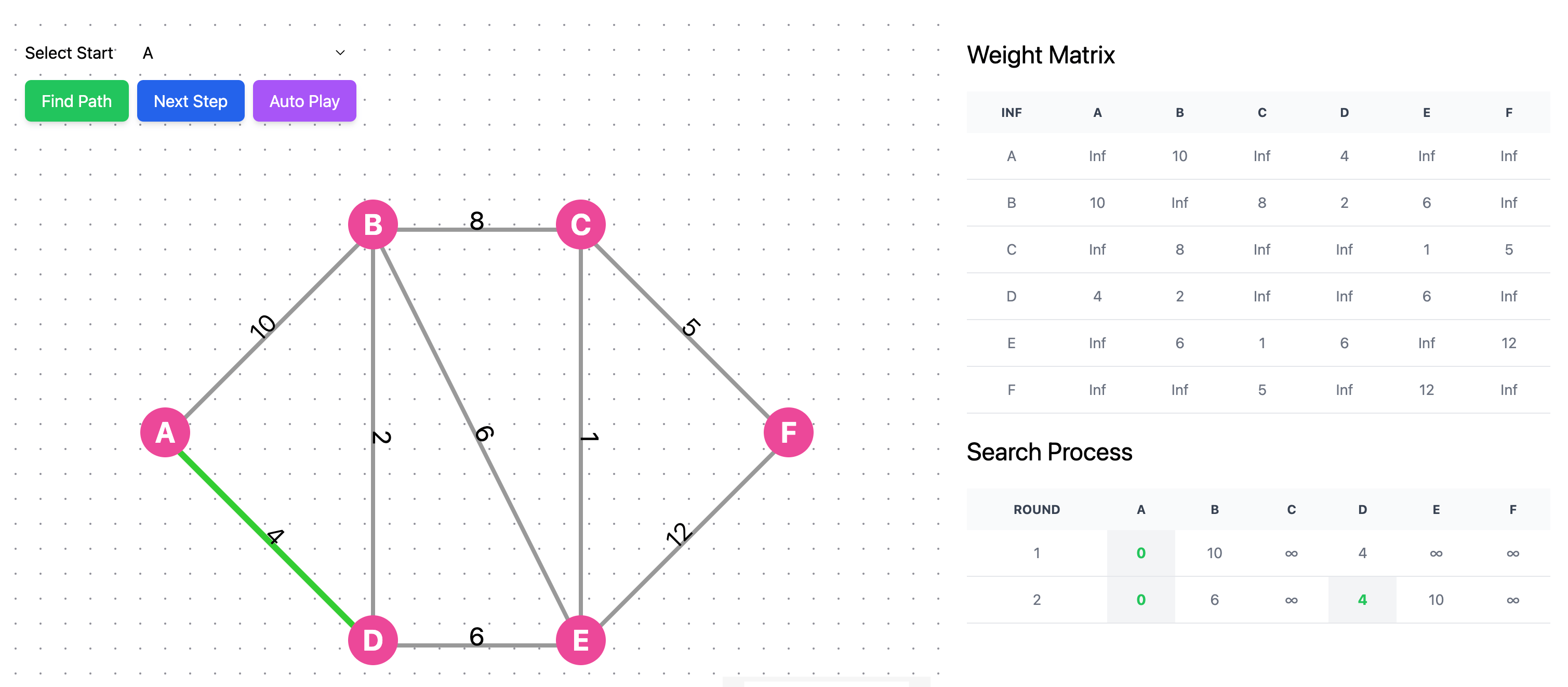
You can see that the distances to both B and E have been updated. B's distance was updated from 10 to 6, and E's distance from infinity to 4.
You can continue to the next step, observing the search process here, watching how the distance numbers and searched vertices change. The final result is as follows:
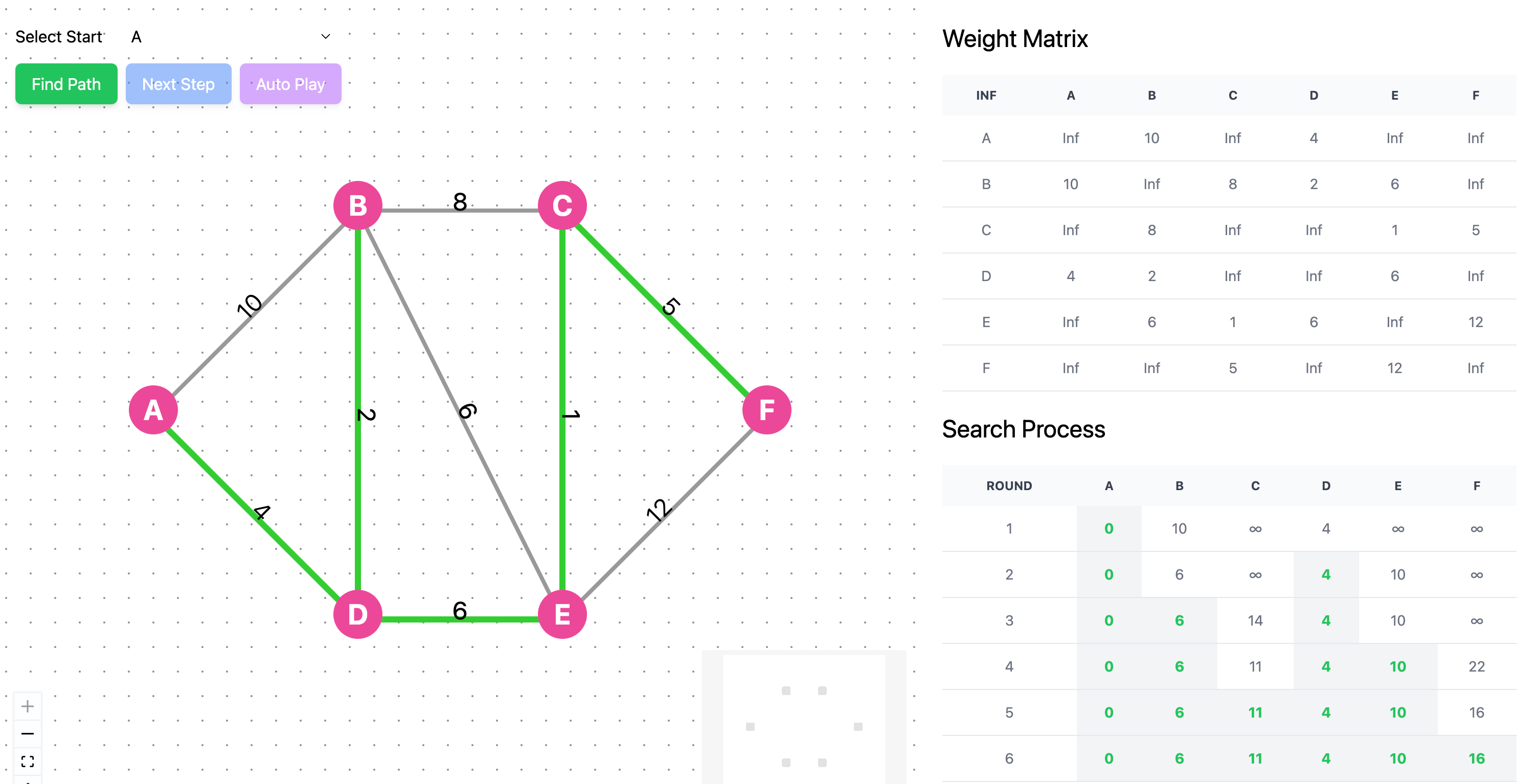
Proof of Dijkstra's Algorithm Correctness
We'll use mathematical induction and proof by contradiction to prove the correctness of Dijkstra's algorithm. At step k of the algorithm, for each vertex v in the visited set T, the distance dist[v] equals the global shortest path length short[v] from the source.
The inductive proof proceeds as follows:
1. Base Case: When k = 1, T only contains the source vertex s, dist[s] = short[s] = 0, so the proposition holds for k = 1.
2. Inductive Hypothesis: Assume the proposition holds at step k, meaning all dist values for vertices in T are the shortest path lengths.
3. Inductive Step: Prove the proposition holds for step k+1:
- Let v be the vertex selected at step k+1 (v has the minimum dist value among unvisited vertices); v is connected to some vertex u in set T
- Need to prove: dist[v] = short[v]
Using proof by contradiction:
- Assume there exists a path P from source s to v with length short[v], where short[v] < dist[v]
- Since source s is in set T and vertex v is not, path P must pass through at least one vertex in set T (besides the source). This is because any distance from s to vertices not in T must be calculated and updated through vertices in T
- Let last be the final vertex in set T along path P, followed by vertex y in the unvisited set to reach v. Let's analyze path P's length:
short[v] = dist[last] + distance[last,y] + distance[y,v] // Length of path P
≥ dist[y] + distance[y,v] // By dist[y] update rule
≥ dist[v]
To understand the above derivation, two key points are essential:
- By the inductive hypothesis, dist[last] is the shortest distance to last; for vertex y, by Dijkstra's update rule: dist[y] ≤ dist[last] + distance[last,y]
- Since algorithm chose v as the minimum distance vertex at step k+1, we have dist[v] ≤ dist[y] + distance[y,v]
Thus, we've derived short[v] >= dist[v], which contradicts our assumption short[v] < dist[v]. Therefore, the assumption is false, and dist[v] is indeed the shortest path length from source to v. This proves that the algorithm correctly determines the shortest path length for each selected vertex.
Dijkstra's Algorithm Requires Non-negative Weights
Finally, it's worth noting that Dijkstra's algorithm requires all edge weights in the graph to be non-negative. This is because:
- If negative weight edges exist, the greedy strategy may fail
- After determining a vertex's shortest path, a shorter path might be found through negative weight edges, violating the algorithm's basic assumption: confirmed shortest paths won't be updated
For example, in the graph below, there's a negative weight edge CE with weight -13. The actual shortest path to E is 1 (shown by red arrows), but the algorithm calculates it as 10:
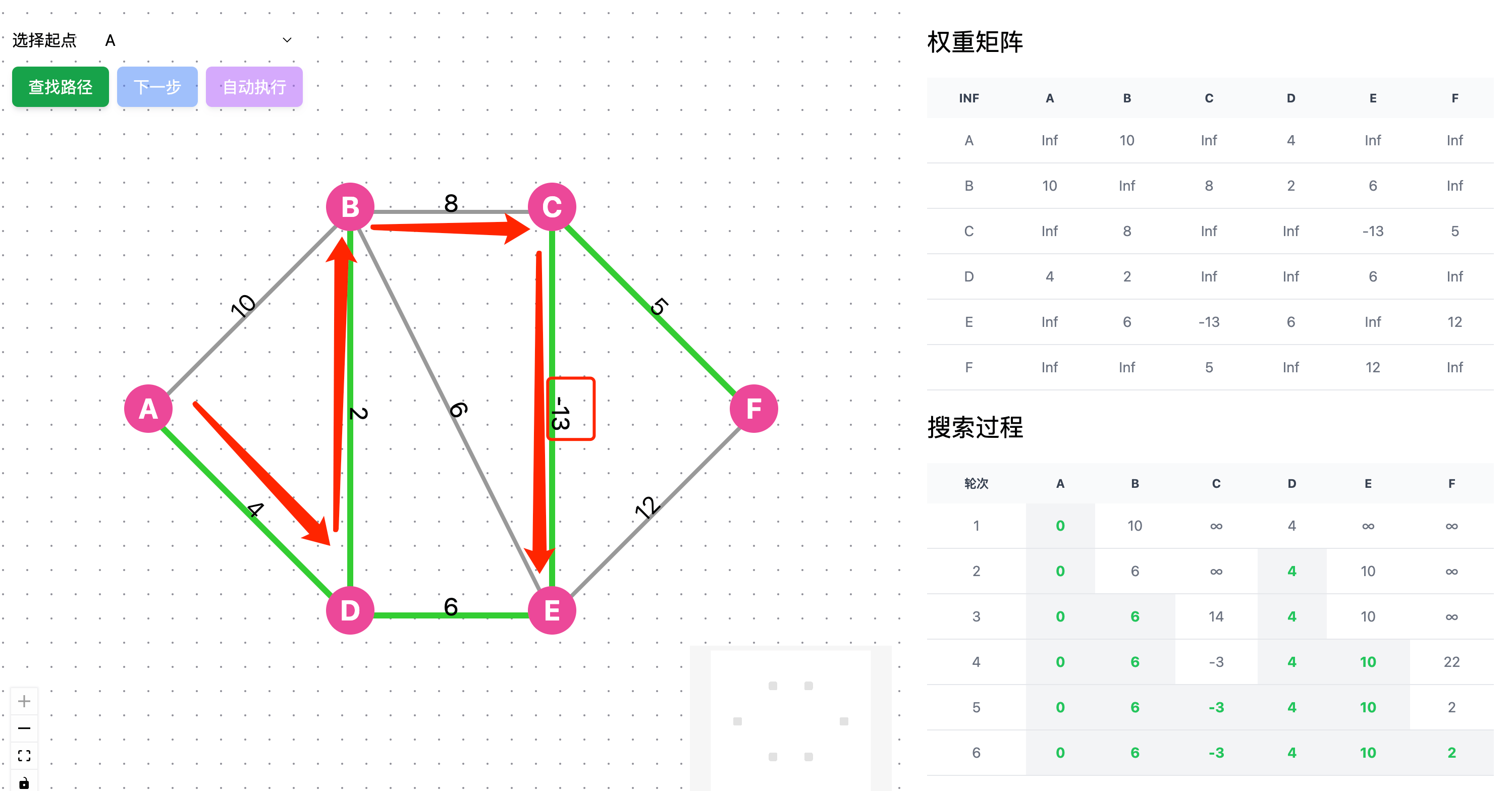
For graphs with negative weight edges, other algorithms (such as the Bellman-Ford algorithm) must be used to solve the shortest path problem.