A Binary Search Tree (BST) is a special type of binary tree data structure with the following characteristics:
- Each node contains a value (key)
- All nodes in the left subtree have values less than the current node's value
- All nodes in the right subtree have values greater than the current node's value
- Both left and right subtrees are also binary search trees
Binary Search Tree Visualization
This page provides an interactive Binary Search Tree visualization tool to help understand the structure and operational principles of BSTs.
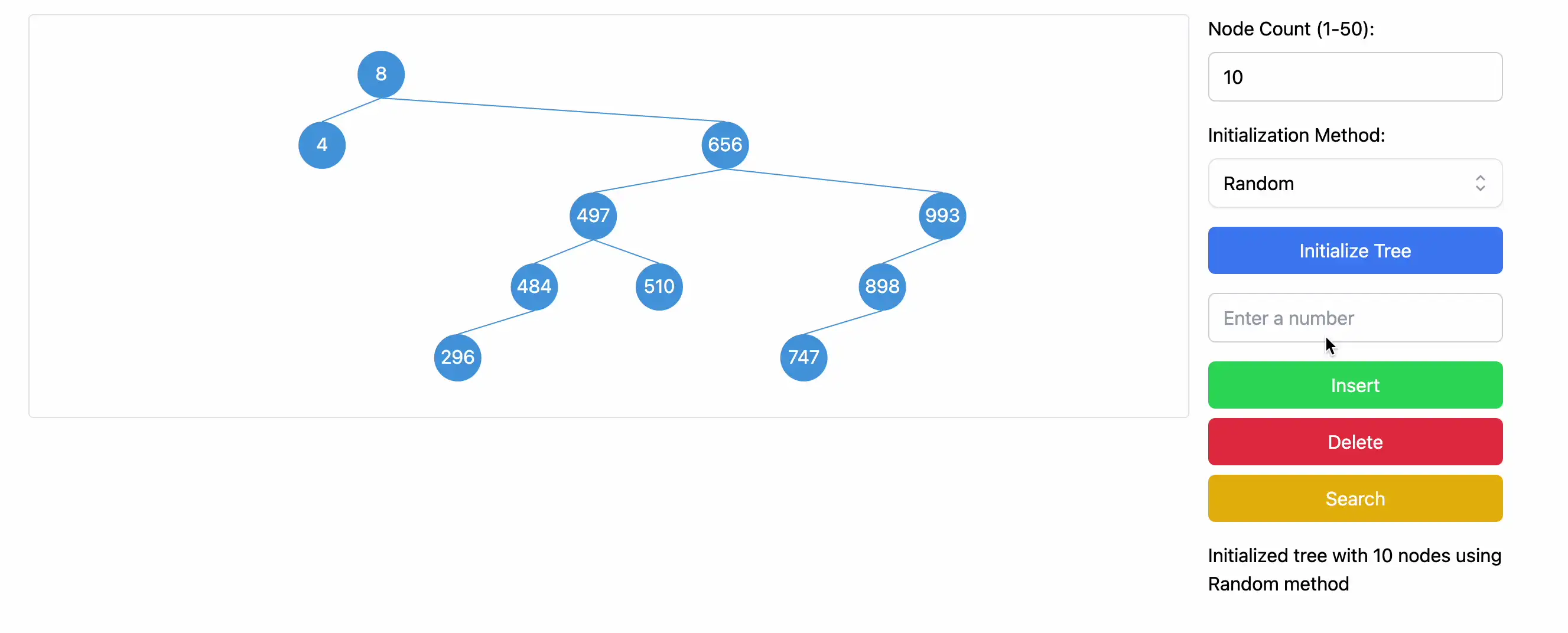
Tree Initialization
When starting to use the visualization tool, you can first initialize a binary search tree. The page provides flexible initialization options, allowing users to specify the tree size from 1 to 50 nodes. This range allows demonstration of both simple tree structures and more complex scenarios.
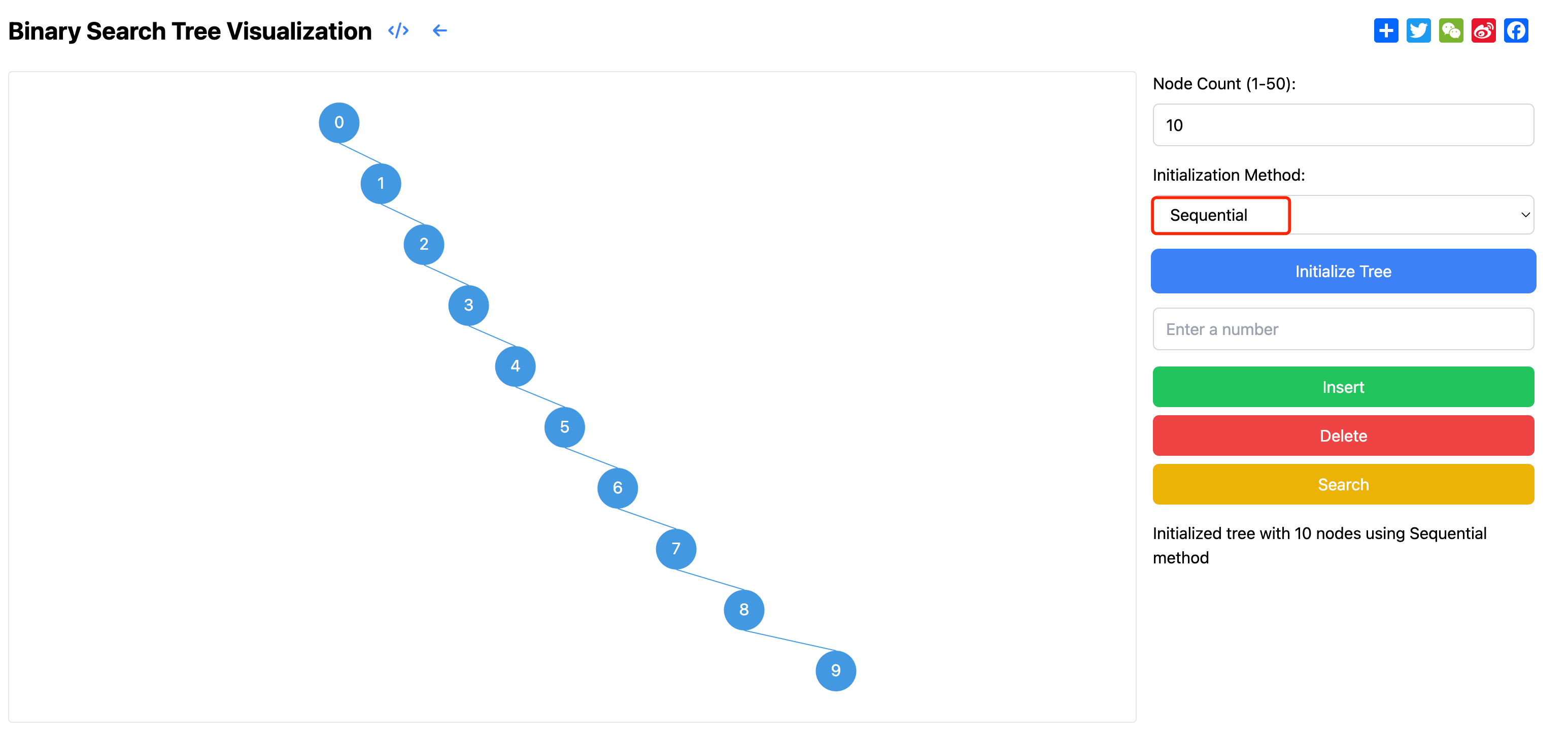
Initialization supports two different value generation methods. The first is random value mode, where the system generates unique random numbers between 1 and 1000 as node values. This mode simulates real-world random data scenarios, showing tree formation under different data distributions. The second is sequential value mode, where the system generates node values in sequence (0,1,2...). This mode is particularly helpful in understanding potential tree degradation when handling ordered data.
The visualization tool implements three core BST operations, each showing real-time changes in tree structure.
Search and Insertion
The search operation demonstrates the efficient lookup advantage of BSTs. When searching for a value in a BST, we start from the root node and use the BST property (all left subtree values less than root, all right subtree values greater than root) to narrow down the search range:
- If the target value equals the current node's value, we've found the target node
- If the target value is less than the current node's value, continue searching in the left subtree
- If the target value is greater than the current node's value, continue searching in the right subtree
This approach eliminates approximately half the nodes with each comparison, greatly improving search efficiency. Users can input any value to search, and the system will highlight the complete search path, visually demonstrating the entire lookup process from root to target position.
The insertion operation allows users to add new nodes to the BST. The system automatically finds the appropriate position while maintaining BST properties. The insertion process follows these steps:
- Start at the root node, compare the new value with the current node's value
- If the new value is less than the current node's value, continue searching in the left subtree
- If the new value is greater than the current node's value, continue searching in the right subtree
- When reaching an empty position, that's where the new node should be inserted
Through animation, users can clearly observe how new nodes find their correct positions. This process demonstrates how BSTs grow and expand while maintaining their basic properties (ordering).
An important feature of the insertion operation is that it always adds new nodes at leaf positions, minimizing impact on the existing tree structure. Additionally, by following BST properties during insertion, the process naturally maintains the correct ordering of all nodes.
Deletion Operation
The deletion operation in BSTs is the most complex of the three basic operations, as removing nodes may disrupt the tree structure and require readjustment to maintain BST properties. The deletion operation has three different cases based on the number of child nodes.
-
Deleting a Leaf Node: This is the simplest case. When deleting a leaf node, we first search down the tree to find the target node. Once found, we simply set its parent's corresponding pointer (left or right child) to null. If deleting the root node, we set root to null. This case doesn't affect other parts of the tree since leaf nodes have no children and require no node reconnection.
-
Deleting a Node with One Child: When deleting a node with one child, we first search for the node to delete and determine whether it's a left or right child of its parent. Then, we connect the node's only child (either left or right) directly to the deleted node's parent at the corresponding position. If deleting the root node, its only child becomes the new root. This case involves minimal tree structure changes, requiring only one node reconnection.
-
Deleting a Node with Two Children: This is the most complex case, as we need to find a suitable node to replace the deleted node while maintaining BST properties. The deletion process involves:
- First, find the successor node of the node to be deleted, which is the minimum node in the right subtree. To find the successor: visit the right child of the node to be deleted, then keep going left until reaching a node with no left child. This is the successor node, whose value is just greater than the deleted node's value.
- After finding the successor node, copy its value to the deleted node's position. Then delete the successor node itself. Since the successor node can have at most one right child (it cannot have a left child, otherwise it wouldn't be the minimum), we can delete it using case one or two.
The following figure demonstrates the animation process of deleting a node with 1 child.

Time Complexity Analysis
The performance of a BST is closely related to its structure. In ideal cases, when the tree maintains good balance, BSTs provide highly efficient operation performance.
On average, basic BST operations achieve logarithmic time complexity. Search operations have O(log n) time complexity because each comparison halves the search range, creating a typical binary search process. Insertion operations also have O(log n) time complexity, as they require searching to determine the insertion position followed by constant-time node linking operations. Although deletion operations may involve successor node search and tree reorganization, they still maintain O(log n) time complexity.
However, in the worst case, when a BST degrades into a linked list, its performance significantly deteriorates. This typically occurs when inserting nodes in sorted sequence, such as inserting 1,2,3,4,5 in order. In this case, each new node is inserted at the bottom of the right subtree, causing the tree to completely lose balance and become a single linked list structure. In such degraded cases, all basic operations degrade to O(n) time complexity, as each operation requires traversing the entire list.
Furthermore, in scenarios requiring frequent modifications, numerous insertion and deletion operations may cause the tree structure to gradually become unbalanced. While this can be addressed through periodic tree rebuilding, such solutions incur additional performance overhead. This characteristic makes regular BSTs less suitable for scenarios requiring frequent data updates.
Alternative Data Structures
When BSTs cannot meet performance requirements, we can consider more advanced data structures. These structures are improvements and optimizations based on BSTs, each with specific application scenarios.
AVL Trees: AVL trees are the first self-balancing BSTs invented, maintaining balance by strictly controlling height differences between left and right subtrees. In AVL trees, the height difference between any node's left and right subtrees cannot exceed 1. This strict balancing condition ensures the tree height always remains at O(log n) level. After each insertion or deletion operation, AVL trees restore balance through rotation operations.
Red-Black Trees: These are weakly balanced BSTs that maintain balance by coloring nodes (red or black) and maintaining specific color rules. Compared to AVL trees, red-black trees have more relaxed balance conditions, ensuring only that the longest path from root to leaf is no more than twice the length of the shortest path. This design greatly reduces the number of operations needed to maintain balance while ensuring sufficient performance.
Due to this good balance between equilibrium and performance, red-black trees are widely used in practical engineering. For example, Java's TreeMap and TreeSet, C++'s map and set, and Linux kernel's completely fair scheduler all use red-black trees as their underlying data structure.
B-Trees and B+ Trees: Multi-way search trees specially designed for external storage devices like disks. Unlike binary trees, these trees' nodes can contain multiple keys and children. B-trees store data in all nodes, while B+ trees only store data in leaf nodes, using non-leaf nodes solely as indexes. This structural design significantly reduces the number of disk I/O operations.
Skip Lists: Skip lists are linked list-based data structures that accelerate lookup operations by adding multiple layers of indexes to each node. Skip lists achieve O(log n) time complexity for search, insertion, and deletion operations, making them viable alternatives to balanced BSTs in certain scenarios.